Disclaimer
This blog post is a part of NSA Codebreaker 2024 writeup.
The challenge content is a PURELY FICTIONAL SCENARIO created by the NSA for EDUCATIONAL PURPOSES only. The mention and use of any actual products, tools, and techniques are similarly contrived for the sake of the challenge alone, and do not represent the intent of any company, product owner, or standards body.
Any similarities to real persons, entities, or events is coincidental.
Synopsis
The recovered data indicates the APT is using a DNS server as a part of their operation. The triage team easily got the server running but it seems to reply to every request with errors.
You decide to review past SIGINT reporting on the APT. Why might the APT be targeting the Guardian Armaments JCTV firmware developers? Reporting suggests the APT has a history of procuring information including the location and movement of military personnel.
Just then, your boss forwards you the latest status update from Barry at GA. They found code modifications which suggest additional DNS packets are being sent via the satellite modem. Those packets probably have location data encoded in them and would be sent to the APT.
This has serious implications for national security! GA is already working on a patch for the firmware, but the infected version has been deployed for months on many vehicles.
The Director of the NSA (DIRNSA) will have to brief the President on an issue this important. DIRNSA will want options for how we can mitigate the damage.
If you can figure out how the DNS server really works maybe we will have a chance of disrupting the operation.
Find an example of a domain name (ie. foo.example.com.) that the DNS server will handle and respond with NOERROR and at least 1 answer.
Prompt
Enter a domain name which results in a NOERROR response. It should end with a ‘.’ (period)
Solution
So basically, we start from where we left off at task 5. We recovered 3 files from task 5.
I skip most of the boring forensics part, and I will just go straightforward explaining things.
We will also ignore microservice for now as it will be the focus on Task 7.
Based from the decomplication and context clues, the coredns is built from this project: https://github.com/coredns/coredns
Basically, coredns is a lightweight dns server where you can customize and build features on top of it.
We also saw contents of Corefile
.:1053 {
acl {
allow type A
filter
}
view firewall {
expr type() == 'A' && name() matches '^x[^.]{62}\\.x[^.]{62}\\.x[^.]{62}\\.net-jl7s7rd2\\.example\\.com\\.$'
}
log
cache 3600
errors
frontend
}
Again, based on context clues, this somehow indicates that this is a communication / exfiltration server over DNS.
I want to thank IDA as it is really great in function naming.
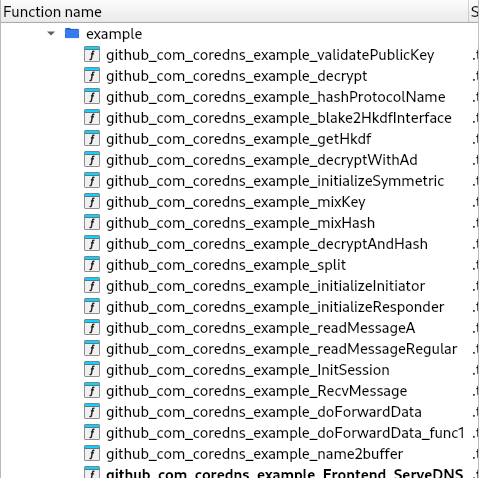
Further research somehow suggest that this might be NOISE PROTOCOL based on function names.
However, I am struggling to find the specific pattern of this protocol until I saw this…
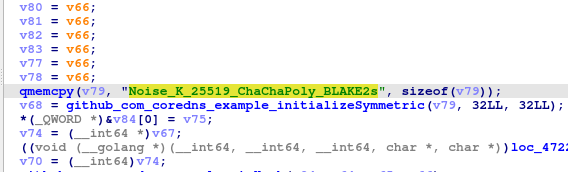
Noise_K_25519_ChaChaPoly_BLAKE2s
During my research, I was able to find this: https://noiseexplorer.com/patterns/K/. Suddenly, we are able to see a clear source code which the binary was probably built from.
Upon digging more in the binary, we are able to learn that there are hard coded keys.
In the initializeResponder, we setup breakpoint in the 2nd mixHash call so we can check the passed arguments, which we can find the initiator’s public key.
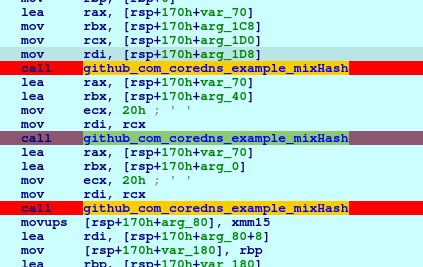

And the 3rd mixHash will contain the public key and the private key of responder.

This one is the responder private key:
var responderPrivateKey = [32]byte{
0xD3, 0xDA, 0x9E, 0x41, 0xB9,
0x75, 0x55, 0x35, 0xAE, 0x62,
0x12, 0x37, 0xEC, 0x7C, 0x2B,
0x77, 0x0D, 0xA0, 0x4A, 0x83,
0x4A, 0xE6, 0x59, 0xF5, 0x80,
0xB0, 0x99, 0x3B, 0x2C, 0xB1,
0x69, 0xDD,
}This one is the initiator public key:
var initiatorPublicKey = [32]byte{
0xB6, 0xB0, 0x1E, 0x07, 0xB1,
0xD4, 0xB1, 0x1E, 0x71, 0xA6,
0x37, 0x6C, 0xE5, 0xEA, 0x49,
0x55, 0xFF, 0x70, 0x3D, 0xF0,
0xFE, 0x9E, 0xC4, 0xB7, 0x3E,
0xDB, 0xB4, 0xA0, 0xE2, 0x64,
0x46, 0x09,
}So, what’s with the Noise K, initiator, and responder?
Basically, K is a pattern that is a one way.
Initiator is the one who will create a message, and responder (server) is the receiver.
But in our case, the server, do not directly communicate back with the initiator.
Based on the context clues, the compromised devices that beacon to this server do have their own private and public key. We can see in the server’s binary that it expects from specific public key.
The compromised devices also have the server’s public key in them to successfully craft a valid message.
So to recap:
- We got the server’s (responder) private key and based from that, we can deduce the public key.
- We also got the client’s (initiator) public key but no private key.
Idea#1
Bruteforce the 128-bit private key.
I did made CUDA bruteforcer, but based on projection, it will take another universe’ big bag before it finish as I do not have quantum computer in my closet.
Idea#2
Maybe the private key was baked in the binary and/or previous binaries provided.
nah.
So what?
Okay, so I’ve totally run out of ideas. I was examining the noise source code, and something really catches my attention. It is the forbiddenCurveValues.
I spent a lot of time researching what the heck are the weakness of the curves, specifically, 25519.
Until I found out this: https://www.iacr.org/archive/ches2011/69170143/69170143.pdf
And this: https://hacken.io/insights/secure-ecdh/
I won’t pretend that I fully understand all of text written in those researches.
But basically, we will be using small-order public key to carry out the attack. The small-order public key’s could reveal predictable results and possibly reconstruct the keys.
Here is the snippet of the exploit process.
/* ---------------------------------------------------------------- *
* EXPLOIT IMPLEMENTATION *
* ---------------------------------------------------------------- */
func main() {
// Known prologue (assuming empty for this example)
prologue := []byte{}
// Responder's public key (computed from private key)
var responderPublicKey [32]byte
curve25519.ScalarBaseMult(&responderPublicKey, &responderPrivateKey)
responderPrivateKeyHex := hex.EncodeToString(responderPrivateKey[:])
fmt.Println("responderPrivateKey (hex):", responderPrivateKeyHex, "\n")
responderPublicKeyHex := hex.EncodeToString(responderPublicKey[:])
fmt.Println("responderPublicKey (hex):", responderPublicKeyHex, "\n")
initiatorPublicKeyHex := hex.EncodeToString(initiatorPublicKey[:])
fmt.Println("initiatorPublicKey (hex):", initiatorPublicKeyHex, "\n")
// Initialize symmetric state as responder
name := []byte("Noise_K_25519_ChaChaPoly_BLAKE2s")
ss := initializeSymmetric(name)
mixHash(&ss, prologue)
mixHash(&ss, initiatorPublicKey[:])
mixHash(&ss, responderPublicKey[:])
// Simulate responder's processing of the message
// hs.re is the small order point we send
hsRe := smallOrderPublicKey
hsReHex := hex.EncodeToString(hsRe[:])
fmt.Println("hsRe (hex):", hsReHex, "\n")
mixHash(&ss, hsRe[:])
// Compute dh(hs.s.privateKey, hs.re)
dh1 := dh(responderPrivateKey, hsRe)
dh1Hex := hex.EncodeToString(dh1[:])
fmt.Println("dh1 (hex):", dh1Hex, "\n")
// MixKey with dh1
mixKey(&ss, dh1)
// Compute dh(hs.s.privateKey, hs.rs)
dh2 := dh(responderPrivateKey, initiatorPublicKey)
responderPrivateKeyHex2 := hex.EncodeToString(responderPrivateKey[:])
fmt.Println("responderPrivateKey (hex):", responderPrivateKeyHex2, "\n")
initiatorPublicKeyHex2 := hex.EncodeToString(initiatorPublicKey[:])
fmt.Println("initiatorPublicKey (hex):", initiatorPublicKeyHex2, "\n")
dh2Hex := hex.EncodeToString(dh2[:])
fmt.Println("dh2 (hex):", dh2Hex, "\n")
// MixKey with dh2
mixKey(&ss, dh2)
// At this point, ss.ck and ss.cs.k contain the chain key and cipher key the responder will use
// Now, as the attacker (initiator), we can compute the same keys
// Initialize symmetric state as initiator
initSS := initializeSymmetric(name)
mixHash(&initSS, prologue)
mixHash(&initSS, initiatorPublicKey[:])
mixHash(&initSS, responderPublicKey[:])
// We use the same hs.e.publicKey (small order point)
hsEPublicKey := smallOrderPublicKey
mixHash(&initSS, hsEPublicKey[:])
// Since we don't have the initiator's private key, but we can set it to zero
var zeroPrivateKey [32]byte
// Compute dh(hs.e.privateKey, hs.rs) with zero private key
dh1Initiator := dh(zeroPrivateKey, responderPublicKey)
mixKey(&initSS, dh1Initiator)
// Compute dh(hs.s.privateKey, hs.rs) with zero private key
dh2Initiator := dh(zeroPrivateKey, responderPublicKey)
mixKey(&initSS, dh2Initiator)
// Now, initSS.ck and initSS.cs.k are the keys the initiator would have
// However, since we used zero private keys, the dh outputs are zeros
// But we know the responder's keys from earlier, so we can use those
// For the exploit, we'll use the responder's ss.ck and ss.cs.k to encrypt the payload
payload := []byte("Secret message from initiator")
// Encrypt the payload using the responder's cipher key and handshake hash
ciphertext := encrypt(ss.cs.k, ss.cs.n, ss.h[:], payload)
ss.cs.n = incrementNonce(ss.cs.n)
// Prepare the message buffer to send to the responder
message := messagebuffer{
ne: smallOrderPublicKey, // Our crafted ephemeral public key
ns: []byte{}, // No static key sent
ciphertext: ciphertext,
}
// The responder will process the message using their state
// For demonstration, we can show that the responder can decrypt the message
// Responder decrypts the ciphertext
valid, _, decryptedPayload := decrypt(ss.cs.k, ss.cs.n-1, ss.h[:], message.ciphertext)
if valid {
fmt.Println("Responder decrypted the message successfully:")
fmt.Println(string(decryptedPayload))
} else {
fmt.Println("Responder failed to decrypt the message.")
}
responderSession := InitSession(false, prologue, keypair{responderPublicKey, responderPrivateKey}, initiatorPublicKey)
_, plaintext, valid, err := RecvMessage(&responderSession, &message)
if err != nil {
panic(err)
}
if !valid {
panic("Decryption failed!")
}
// Output the decrypted message
fmt.Printf("Responder decrypted message: %s\n", string(plaintext))
encode_msg(message)
}Full Solution
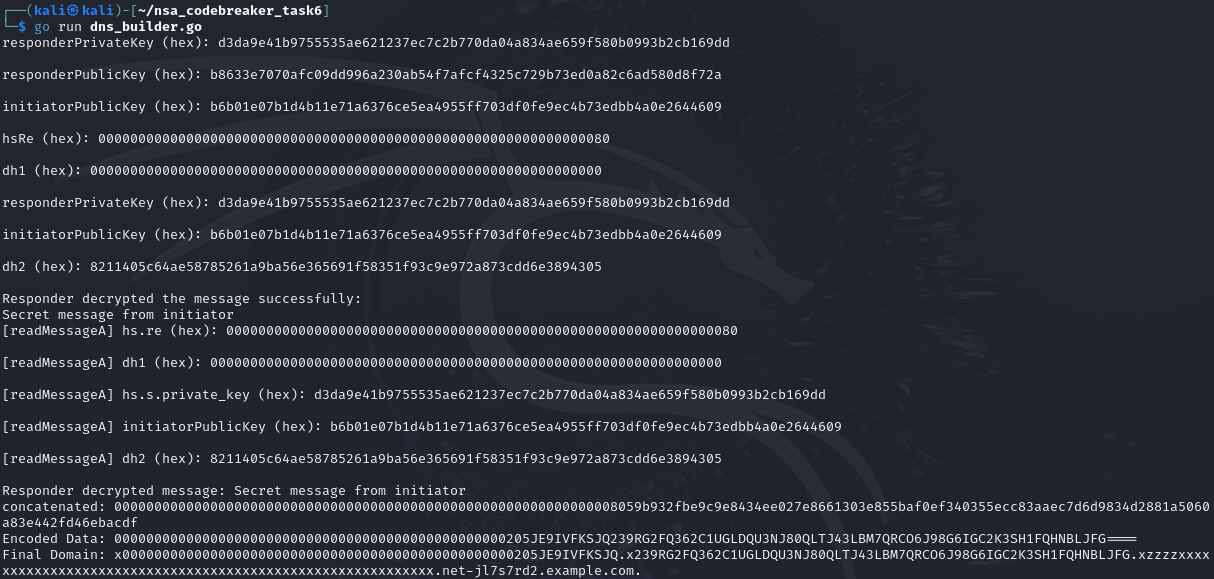
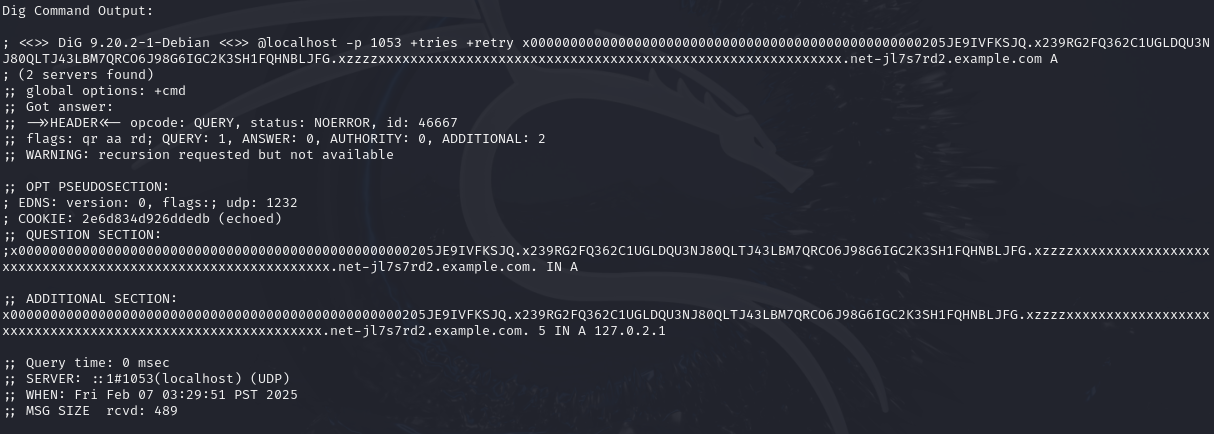
Based on the prompt, we just need to submit a valid domain that will be successfully decrypted by the server (responder).
We can submit this example:
x0000000000000000000000000000000000000000000000000205JE9IVFKSJQ.x239RG2FQ362C1UGLDQU3NJ80QLTJ43LBM7QRCO6J98G6IGC2K3SH1FQHNBLJFG.xzzzzxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx.net-jl7s7rd2.example.comUpon further investigation, we can confirm that after successful decoding of data, it forwards to port 3000 with http protocol. However, payload structure is not yet known and will be the focus for Task 7.
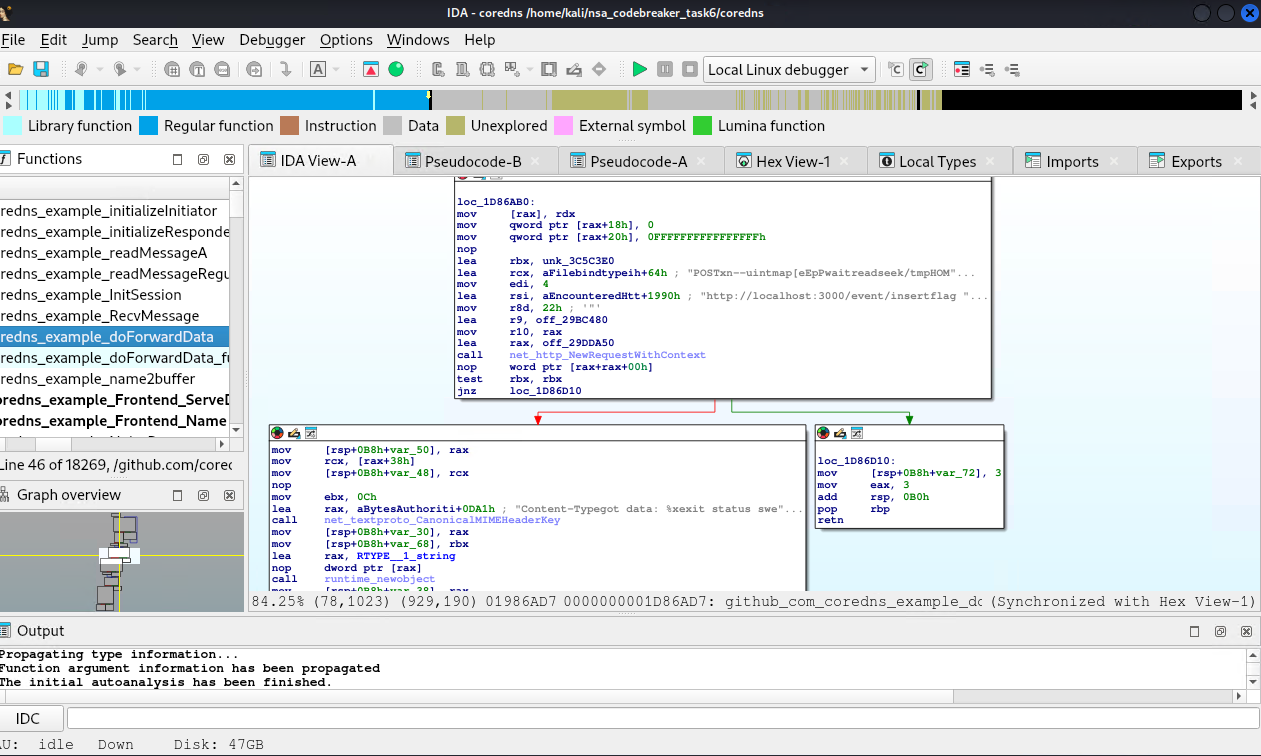
Bonus#1
How did I know that the initial encoding is base32 with 0-9A-V?
Put a breakpoint at name2buffer DecodeString function.

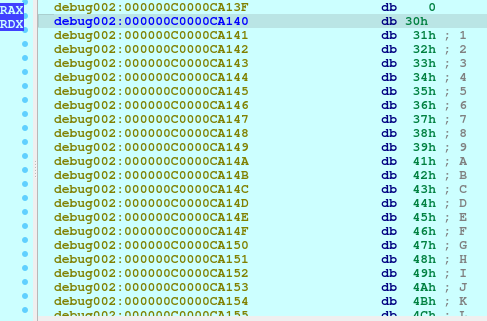
Basically, name2buffer contain statements that we used in ProcessAndDig and encode_msg function on our script.
Bonus#2
Here is a sagemath script to generate low order point for x-coordinate. In theory, few of public keys here that are not included on forbiddenCurveValues should work for the exploit.
p = 2^255 - 19
F = GF(p)
E = EllipticCurve(F, [0, 486662, 0, 1, 0]) # Curve25519
def find_small_order_x_coordinates(d):
try:
psi_d = E.division_polynomial(d)
return [Integer(root) for root in psi_d.roots(multiplicities=False)]
except:
return []
orders = [2, 4, 8]
small_order_x = set()
# Collect x-coordinates from division polynomials
for d in orders:
x_coords = find_small_order_x_coordinates(d)
small_order_x.update(x_coords)
# Add special-case values (explicit Integer conversion)
special_x = [
0, # x=0 (order 4)
1, # x=1 (invalid point)
2^255, # x=2²⁵⁵ (invalid field element)
19, # x=19 (equivalent to 2²⁵⁵ mod p)
0x7FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFED,
0x7FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEE
]
for x in special_x:
small_order_x.add(Integer(x))
# Convert to little-endian byte arrays
def int_to_le_bytes(n):
return list(int(n).to_bytes(32, 'little'))
forbidden_curve_values = [int_to_le_bytes(x) for x in small_order_x]
# Print in Go slice format
print("var forbiddenCurveValues = [][]byte{")
for entry in forbidden_curve_values:
byte_str = ", ".join(f"{b}" for b in entry)
print(f"\t{{{byte_str}}},")
print("}")